Continuous Deformations of Implicit Surfaces
Martinez Esturo, J. and Rössl, C. and Theisel, H.

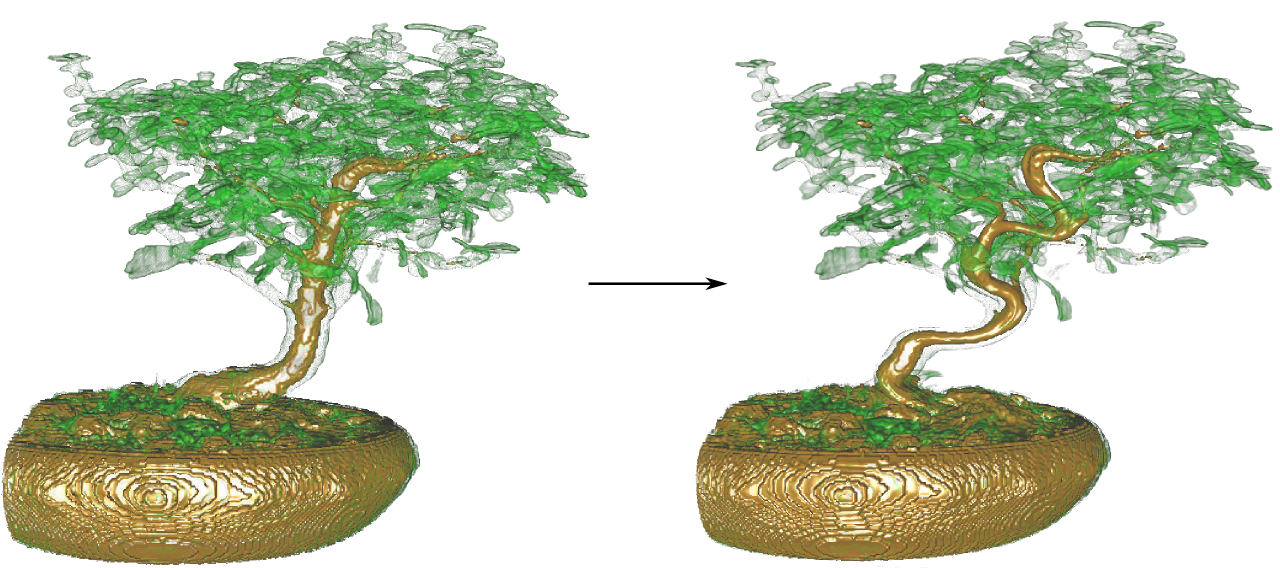
Abstract

We introduce an approach for the continuous deformation of implicit surfaces which considers properties of all isosurfaces of a volume data set simultaneously. This is achieved by integrating divergence-free vector fields which is carried out by an efficient backward Lagrangian integration scheme. Our deformation guarantees volume preservation inside each isosurface as well as the preservation of continuity and topology of every isosurface. For visualization and interaction, we offer a real-time mode that allows interactive working on the resolution of the underlying volumetric grid as well as a grid resolution independent mode offering exact extraction of arbitrary isosurfaces. We apply the approach to the deformation of measured volume data sets as well as to the design of complex implicit shapes with a simple pre-defined topology.

Video

BibTeX

@inproceedings{MartinezEsturo2010,
  title = {Continuous Deformations of Implicit Surfaces},
  author = { {Martinez~Esturo}, J. and R{\"o}ssl, C. and Theisel, H.},
  booktitle = {Proc. VMV},
  pages = {219--226},
  year = {2010},
  publisher = {EG}
}

Data